ML
分类
监督学习(datasets有label)=> 训练模型
- 分类
- 回归
无监督学习(datasets无label)=> 对数据做处理
- 聚类 (分类)
- 将维 (特征提取,压缩)
- 应用:减少无用featuers,方便可视化,异常检测
半监督学习(datasets有的有label,有的无label)
增强学习(根据环境action)
Action => Environment => State: Reward/Reject ^ | | | ------------------- 根据周围环境情况采取行动,再根据行动结果(奖/惩),学习行为方式,如此往复,不断学习
机器学习过程
- 训练数据集
X_train,y_train=> fit 拟合训练数据集 => 模型 - 输入样例
x=> 模型 => predict 结果
判断算法性能
- 训练和测试数据集分离(train_test_split),使用测试数据判断模型好坏
- 准确度 accuracy
模型参数 & 超参数
- 模型参数:算法过程中学习的参数
- 超参数: 算法运行前需要决定的参数(=>需调参)
- 寻找好的超参数:
- 领域知识
- 经验数值
- 实验搜索(eg: 网格搜索)
scikit-learn提供GridSearch网格搜索方法(封装在sklearn.model_selection包中),实验搜索好的超参数
- 寻找好的超参数:
样本表示
- 每个样本用一个向量表示 => 一维数组
- 每个样本有1~n个特征(features) => 一维数组的size
- m个样本 => m*n矩阵,用一个二维数组表示
- m: 行, samples
- n: 列, features
样本间距离
有不同的计算方式, eg:
向量的范数:
- 曼哈顿距离 (1维空间) : $ (\sum_{i=1}^n{|X_i^a-X_i^b|})^\frac{1}{1} $ (两个点在每个维度上相应距离的和)
- 欧拉距离 (2维空间) : $ (\sum_{i=1}^n{|X_i^a-X_i^b|^2})^\frac{1}{2} $
- ( $ \sqrt{\sum_{i=1}^n{(X_i^a-X_i^b)^2}} $ )
- 明可夫斯基距离 (p维空间) : $ (\sum_{i=1}^n{|X_i^a-X_i^b|^p})^\frac{1}{p} $
统计学上的相似度:
- 向量空间余弦相似度 (Cosine Similarity)
- 调整余弦相似度 (Adjusted Cosine Similarity)
- 皮尔森相关系数 (Pearson Correlation Coefficient)
- Jaccard相似系数 (Jaccard Coefficient)
维数灾难
随着维度的增加,“看似相近”的两个点之间的距离越来越大
| 维数 | 两个样本 | 两样本间的距离 |
|---|---|---|
| 1维 | 0 & 1 | 1 |
| 2维 | (0,0) & (1,1) | 1.414 |
| 3维 | (0,0,0) & (1,1,1) | 1.73 |
| 64维 | (0,0,...,0) & (1,1,...,1) | 8 |
| 10000维 | (0,0,...,0) & (1,1,...,1) | 100 |
优化方法:将维
scikit-learn
提供标准数据集和6大基本功能 ( Documents | API Reference )
标准数据集
小数据集
数据集名称 调用方式 适用算法 数据规模 波士顿房价数据集 load_boston()回归 506*13 糖尿病数据集 load_diabetes()回归 442*10 鸢尾花数据集 load_iris()分类 150*4 手写数字数据集 load_digits()分类 5620*64 大数据集
数据集名称 调用方式 适用算法 数据规模 Olivetti脸部图像数据集 fetch_olivetti_faces()降维 400_64_64 新闻分类数据集 fetch_20newsgroups()分类 - 带标签的人脸数据集 fetch_lfw_people()分类;降维 - 路透社新闻语料数据集 fetch_rcv1()分类 804414*47236 注: 小数据集可以直接使用,大数据集要在调用时程序自动下载(一次即可)
示例:数据集之鸢尾花
加载数据集
from sklearn import datasets iris=datasets.load_iris() # 加载鸢尾花数据集 iris.keys() # dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename']) iris.DESC # 1. `.DESC` : some description iris.feature_names # 2. `.feature_names`: each feature meaning ''' ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] ''' iris.target_names # 3. `.target_names`: each target meaning ''' array(['setosa', 'versicolor', 'virginica'], dtype='<U10') ''' X = iris.data # 4. `.data` : features (x1,x2,x3,x4) y = iris.target # 5. `.target` : result labels (y1,y2,y3)可视化
- 取前两个feature(x1 & x2) 绘制散点图 => 发现基本可以区分出y=0的花
plt.scatter(X[y==0,0],X[y==0,1],color="red",marker="o") plt.scatter(X[y==1,0],X[y==1,1],color="blue",marker="+") plt.scatter(X[y==2,0],X[y==2,1],color="green",marker="x")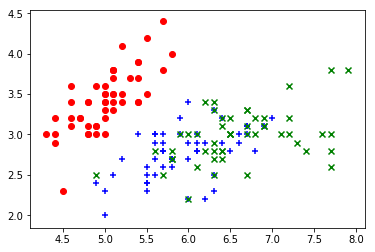
- 取后两个feature绘制散点图 => 发现可区分出y=0的花
plt.scatter(X[y==0,2],X[y==0,3],color="red",marker="o") plt.scatter(X[y==1,2],X[y==1,3],color="blue",marker="+") plt.scatter(X[y==2,2],X[y==2,3],color="green",marker="x")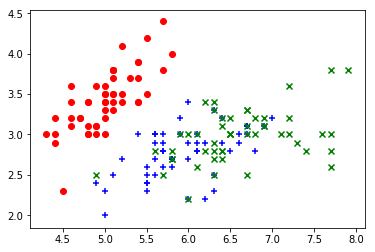
- 取前两个feature(x1 & x2) 绘制散点图 => 发现基本可以区分出y=0的花
基本功能
共分为6大部分,分别用于:
模型选择
model_selection- 数据集分割 (eg:
train_test_split) - 交叉验证 (eg:
cross_validate) - 超参数评估选择 (eg: 网格搜索
GridSearchCV) - ...
- 数据集分割 (eg:
数据预处理
preprocessing- 特征归一化处理 (eg:
MinMaxScaler,StandardScaler) - Normalization
- ...
- 特征归一化处理 (eg:
分类任务
- 最近邻算法
neighbors.NearestNeighbors - 支持向量机
svm.SVC - 朴素贝叶斯
naive_bayes.GaussianNB - 决策树
tree.DecisionTreeClassifier - 集成方法
ensemble.BaggingClassifier - 神经网络
neural_network.MLPClassifier
- 最近邻算法
回归任务
- 岭回归
linear_model.Ridge - Lasso回归
linear_model.Lasso - 弹性网络
linear_model.ElasticNet - 最小角回归
linear_model.Lars - 贝叶斯回归
linear_model.BayesianRidge - 逻辑回归
linear_model.LogisticRegression - 多项式回归
preprocessing.PolynomialFeatures
- 岭回归
聚类任务
- K-means
cluster.KMeans - AP聚类
cluster.AffinityPropagation - 均值漂移
cluster.MeanShift - 层次聚类
cluster.AgglomerativeClustering - DBSCAN
cluster.DBSCAN - BIRCH
cluster.Birch - 谱聚类
cluster.SpectralClustering
- K-means
降维任务
- 主成分分析
decomposition.PCA - 截断SVD和LSA
decomposition.TruncatedSVD - 字典学习
decomposition.SparseCoder - 因子分析
decomposition.FactorAnalysis - 独立成分分析
decomposition.FastICA - 非负矩阵分解
decomposition.NMF - LDA
decomposition.LatentDirichletAllocation
- 主成分分析
数据预处理: 数据集分割
训练测试数据集分离(train_test_split)
自定义
import numpy as np def train_test_split(X,y,test_ratio=0.2,seed=None): ''' 将数据集(X & y) 按照test_radio比例,分割成训练集(X_train & y_train) 和测试集(X_test & y_test) ''' assert X.shape[0] == y.shape[0], "the size of X must be equal to the size of y" assert 0.0 <=test_ratio <=1.0, "test_radio must be valid" if seed: np.random.seed(seed) # 1. shuffle indexes shuffle_indexes = np.random.permutation(X.shape[0]) # 2. test & train shuffled indexes test_size = int(X.shape[0] * test_ratio) test_indexes = shuffle_indexes[:test_size] train_indexes = shuffle_indexes[test_size:] # 3. get test & train array X_test = X[test_indexes] y_test = y[test_indexes] X_train = X[train_indexes] y_train = y[train_indexes] return X_train,X_test,y_train,y_test if __name__ == "__main__": # 1. load datasets from sklearn import datasets iris = datasets.load_iris() X = iris.data y = iris.target # 2. train test split X_train,X_test,y_train,y_test=train_test_split(X,y,test_ratio=0.2) print("X_train:",X_train.shape) print("y_train:",y_train.shape) print("X_test:",X_test.shape) print("y_test:",y_test.shape)scikit-learn中提供的方法(封装在
sklearn.model_selection包中)import numpy as np # 1. load datasets from sklearn import datasets iris = datasets.load_iris() X = iris.data y = iris.target # 2. do train_test_split from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=66) # 3. check X_train.shape # (120, 4) y_train.shape # (120,)
数据预处理: 特征归一化
数据集特征归一化(Feature Scaling)
问题:样本间距离被较大数级的
feature给主导了解决方案:将所有的数据映射到同一尺度
- 最值归一化
normalization:- 将所有数据都映射到
0~1之间 $x_{scale} = \frac{x - x_{min}}{x_{max} - x_{min}}$ - 适用于分布有明显边界(min,max)的情况;受极端数据值(outlier)影响较大
- 将所有数据都映射到
- 均值方差归一化
standardization:- 将所有数据归一到
均值为0,均方差为1的分布中 $x_{scale} = \frac{x - x_{mean}}{x_{std}}$ - 适用于数据分布没有明显的边界;有可能存在极端数据值
- 注:对有明显边界/无极端数据值的数据,这种归一化效果也很好
- 将所有数据归一到
- 最值归一化
注:测试数据集的归一化
- 使用训练数据集的关键数值
- 如:均值方差归一化,使用测试数据的均值
mean_train& 均方差std_train=>(x_test-mean_train)/std_train - 原因:测试数据集是模拟真实环境,真实环境很可能无法得到所有数据的均值和方差,且数据的归一化也算是这个算法的一部分
scikit-learn提供的Scaler归一化方法- 以类的形式封装在
sklearn.preprocessing包中,eg:MinMaxScalerStandardScaler- ...
- 使用流程和机器学习的流程是一致的
- 训练数据集(
X_train) => fit => 保存关键信息的Scalar - 输入样例 => 保存关键信息的
Scalar=> transform 出结果
- 训练数据集(
- 以类的形式封装在
Sample1.1:自实现MinMaxScaler
'''
0~1 最值归一化 normalization: (x-x_min/(x_max-x_min)
'''
class MinMaxScaler:
def __init__(self):
self.min_ = None
self.max_ = None
def fit(self,X):
# 计算保存每个feature(列)的最小最大值
self.min_ = np.min(X,axis=0)
self.max_ = np.max(X,axis=0)
return self
def transform(self,X):
''' 归一化处理 '''
# 元素类型转换为浮点,否则做归一化时会强制为整数,都会变成0
X_scaled=np.empty(shape=X.shape,dtype=float)
# features(列)上做归一化处理
for col in range(X.shape[-1]):
X_scaled[:,col]=(X[:,col]-self.min_[col])/(self.max_[col]-self.min_[col])
return X_scaled
if __name__ == '__main__':
X = np.array([[4, 1, 2, 2],
[1, 3, 9, 3],
[5, 7, 5, 1]])
scaler = MinMaxScaler()
scaler.fit(X)
print("min_:",scaler.min_) # min_: [1 1 2 1]
print("max_:",scaler.max_) # max_: [5 7 9 3]
X_scaled=scaler.transform(X)
print(X_scaled) '''
[[0.75 0. 0. 0.5 ]
[0. 0.33333333 1. 1. ]
[1. 1. 0.42857143 0. ]]
'''
Sample1.2: 自实现StandardScaler
'''
Standarlization 均值方差归一化: (x-x_mean)/x_std
'''
class StandardScaler:
def __init__(self):
self.mean_ = None
self.scale_ = None
def fit(self,X):
''' 计算保存每个feature的均值和均方差 '''
self.mean_ = np.mean(X,axis=0)
self.scale_ = np.std(X,axis=0)
return self
def transform(self,X):
''' 归一化处理 '''
X_scaled=np.empty(shape=X.shape,dtype=float)
for col in range(X.shape[-1]):
X_scaled[:,col]=(X[:,col]-self.mean_[col])/self.scale_[col]
return X_scaled
if __name__ == '__main__':
X = np.array([[4, 1, 2, 2],
[1, 3, 9, 3],
[5, 7, 5, 1]])
scaler = StandardScaler()
scaler.fit(X)
print("mean_:",scaler.mean_) # mean_: [3.33333333 3.66666667 5.33333333 2. ]
print("std_:",scaler.std_) # std_: [1.69967317 2.49443826 2.86744176 0.81649658]
X_scaled=scaler.transform(X)
print(X_scaled)
'''
[[ 0.39223227 -1.06904497 -1.16247639 0. ]
[-1.37281295 -0.26726124 1.27872403 1.22474487]
[ 0.98058068 1.33630621 -0.11624764 -1.22474487]]
'''
Sample2.1: sklearn中的MinMaxScaler
'''
MinMaxScaler
X_std = (X-X.min(axis=0)) / (X.max(axis=0)-X.min(axis=0))
X_scaled = X_std * (max-min)+min
range 0~1 => min=0, max=1
'''
X = np.array([[4, 1, 2, 2],
[1, 3, 9, 3],
[5, 7, 5, 1]])
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X)
minMaxScaler.data_min_ # = np.min(X_train,axis=0)
minMaxScaler.data_max_ # = np.max(X_train,axis=0)
minMaxScaler.scale_ # = (max-min)/(X.max(axis=0)-X.min(axis=0)) = 1/(minMaxScaler.data_max_-minMaxScaler.data_min_)
minMaxScaler.min_ # = min - X.min(axis=0) * self.scale_ = 0 - minMaxScaler.data_min_ * self.scale_
X_scaled = scaler.transform(X)
Sample2.2: sklearn中的StandardScaler
'''
StandardScaler
z = (x - x_mean) / x_std
'''
X = np.array([[4, 1, 2, 2],
[1, 3, 9, 3],
[5, 7, 5, 1]])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X)
standardScaler.mean_ # 均值
standardScaler.scale_ # 均方差 (scale可理解成描述数据分布范围的一个变量,std只是描述数据分布范围的一种统计指标而已)
X_scaled = scaler.transform(X)
Sample3:将sklearn的iris数据集归一化
# 1. load datasets:
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 2. train_test_split
from sklearn.model_selection import train_test_split
X_train,y_train,X_test,y_test=train_test_split(X,y,test_size=0.2,random_state=66)
# 3. 归一化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
# 归一化测试集X_train
X_train_scaled = scaler.transform(X_train)
# 归一化训练集X_test(使用测试集X_train得到的mean & std)
X_test_scaled = scaler.transform(X_test)
模型度量:准确度
准确度(accuracy_score)
自定义
import numpy as np def accuracy_store(y_true,y_predict): assert y_true.shape[0] == y_predict.shape[0], "the size of y_true must be equal to the size of y_predict" return sum(y_true==y_predict)/len(y_true)scikit-learn中提供的方法(封装在
sklearn.metrics包中)from sklearn.metrics import accuracy_score accuracy_score(y_test,y_predict)
kNN - k近邻算法
k-Nearest Neighbors
- 可用于
分类Classify(包括多分类)和回归Regression问题 - scikit-lean封装knn在包
sklearn.neighbors中- 解决分类问题:
KNeighborsClassifier - 解决回归问题:
KNeighborsRegressor - 使用步骤:
- 创建KNN类实例
- 调用fit方法(传入训练集),返回模型(即KNN实例本身)
- 调用predict方法(传入测试集),返回预测结果(向量形式)
- 准确度评估:
- 调用封装在
sklearn.metrics包中的accuracy_score(y_true,y_predict) - 自实现方式:
sum(y_true==y_predict)/len(y_true)
- 调用封装在
- 解决分类问题:
- 模型参数: 较特殊,没有模型参数,实际不需要具体的拟合训练,直接根据训练数据集predict出结果
- 超参数:
n_neighbors= 5 ( 即k)weights=uniform/distance(不考虑距离/考虑距离作为权重)metric=minkowski&metric_params&p=2 (距离度量方式)algorithm=auto/ball_tree/kd_tree/brute&leaf_size=30- Note: minkowski距离(p维空间)= $ (\sum_{i=1}^n{|X_i^a-X_i^b|^p})^\frac{1}{p} $
- 优点:思想简单,效果强大
- 缺点:
- 效率低下: 如果训练集有m个样本,n个特征,则预测每个新数据,需要
O(m*n), 优化:使用树结构(eg:KD-Tree,Ball-Tree) - 高度数据相关: 对outlier更加敏感(结果很大程度上取决于k的选择,在边界处效果不佳)
- 预测的结果不具有可解释性
- 维数灾难: 随着维度的增加,“看似相近”的两个点之间的距离越来越大(优化方法:将维)
- 效率低下: 如果训练集有m个样本,n个特征,则预测每个新数据,需要
Sample: 自实现的KNeighborsClassifier
import numpy as np
from math import sqrt
from collections import Counter
class KNNClassifier:
def __init__(self,k):
''' 初始化kNN分类器 '''
assert k>=1, "k must be valid"
self.k=k
self.__X_train=None
self.__y_train=None
# 1. fit
def fit(self,X_train,y_train):
''' 根据训练集X_train & y_train 训练kNN分类器 '''
assert X_train.shape[0] == y_train.shape[0], "the size of X_train must equal to the size of y_train"
# kNN算法较特殊,实际上并不需要具体的拟合训练过程,可直接根据训练数据集predict出结果
self.__X_train=X_train
self.__y_train=y_train
return self
# 2. predict
def predict(self,X_predict):
''' 对待预测数据集X_predict(矩阵),进行预测,返回预测结果集y_predict(向量) '''
assert self.__X_train is not None and self.__y_train is not None, "must fit before predict!"
assert X_predict.shape[1] == self.__X_train.shape[1], "the feature number of X_predict must be equal to X_train"
y_predict = [self.__predict(x) for x in X_predict]
return np.array(y_predict)
def __predict(self,x):
''' 对单个待预测数据x,进行预测 '''
assert x.shape[0] == self.__X_train.shape[1], "the featuer number of x must be equal to X_train"
distances=[sqrt(np.sum((x_train - x)**2)) for x_train in self.__X_train]
nearest=np.argsort(distances)
topK_y=[self.__y_train[i] for i in nearest[:self.k]]
votes=Counter(topK_y)
# print(votes)
return votes.most_common(1)[0][0]
def __repr__(self):
return "KNN_classify(k=%d)" % self.k
# 3. accuracy_store
def score(self,X_test,y_test):
''' 根据测试数据集(X_test,y_test)确定当前模型的准确度 '''
y_predict=self.predict(X_test)
assert y_test.shape[0] == y_predict.shape[0], "the size of y_test must be equal to the size of y_predict"
return sum(y_test==y_predict)/len(y_test)
if __name__ == "__main__":
# 1. load datasets:
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 2. train_test_split
from sklearn.model_selection import train_test_split
X_train,y_train,X_test,y_test=train_test_split(X,y,test_size=0.2,random_state=66)
print("X_train:",X_train.shape)
print("y_train:",y_train.shape)
print("X_test:",X_test.shape)
print("y_test:",y_test.shape)
# 3. verify KNN
my_knn_clf = KNNClassifier(k=6)
my_knn_clf.fit(X_train,y_train)
y_predict=my_knn_clf.predict(X_test) # 传入要预测的数据集(矩阵形式),返回预测结果集(向量形式)
# 准确度评估
correct_cnt = sum(y_predict==y_test)
accuracy = correct_cnt/len(y_test)
print("correct_cnt:",correct_cnt)
print("accuracy:",accuracy)
Sample: sklean中的KNeighborsClassifier
'''
KNeighborsClassifier(
n_neighbors=5,
weights='uniform',
algorithm='auto',
leaf_size=30,
p=2,
metric='minkowski',
metric_params=None,
n_jobs=None,
**kwargs
)
'''
# 1. load datasets:
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 2. train_test_split
from sklearn.model_selection import train_test_split
X_train,y_train,X_test,y_test=train_test_split(X,y,test_size=0.2,random_state=66)
print("X_train:",X_train.shape)
print("y_train:",y_train.shape)
print("X_test:",X_test.shape)
print("y_test:",y_test.shape)
# 3. use sklearn: KNeighborsClassifier
from sklearn.neighbors import KNeighborsClassifier
knn_clf=KNeighborsClassifier(n_neighbors=6)
knn_clf.fit(X_train,y_train)
y_predict=knn_clf.predict(X_test)
# 可调用accuracy_score方法计算预测值的准确度
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test,y_predict)
print("accuracy:",accuracy)
# KNN类内部也提供score方法(自动调用predict进行预测,然后进行准确度计算,返回准确度)
accuracy = knn_clf.score(X_test,y_test)
print("accuracy:",accuracy)
Sample: sklean中的KNeighborsRegressor
# 1. data
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston()
X = boston.data
y = boston.target
y_max = np.max(y)
X = X[y<y_max]
y = y[y<y_max]
print("X.shape:",X.shape)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=66)
print("X_train.shape:",X_train.shape)
# 2. kNeighborsRegressor
from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train,y_train)
y_predict = reg.predict(X_test)
print("y_predict:",y_predict)
score = knn_reg.score(X_test,y_test) # r2_score
print("score:",score)
Sample: 数据集预处理之特征归一化
数据集特征归一化 (Feature Scaling)后,使用KNN分类
'''
from sklearn import datasets
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train,y_train,X_test,y_test=train_test_split(X,y,test_size=0.2,random_state=66)
'''
# 1. 数据集预处理:均值方差归一化
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train) # 训练数据集 归一化处理
X_test_standard = standardScaler.transform(X_test) # 测试数据集 归一化处理
# 2. KNN分类:使用归一化的数据集
from sklearn.neighbors import KNeighborsClassifier
knn_clf=KNeighborsClassifier(n_neighbors=6)
knn_clf.fit(X_train_standard,y_train)
y_predict=knn_clf.predict(X_test_standard)
# 3. 计算准确度
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test,y_predict)
print("accuracy:",accuracy)
Sample: 使用网格搜索方式,寻找到当前最优的超参数
加载使用模型选择model_selection模块的网格搜索GridSearchCV (CV: cross validation)
'''
KNeighborsClassifier(
n_neighbors=5,
weights='uniform',
algorithm='auto',
leaf_size=30,
p=2,
metric='minkowski',
metric_params=None,
n_jobs=None,
**kwargs
)
# 加载数据
from sklearn import datasets
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train,y_train,X_test,y_test=train_test_split(X,y,test_size=0.2,random_state=66)
'''
from sklearn.model_selection import GridSearchCV
# 这里考虑3个超参数:n_neighbors,weights,p
param_grid=[
{
'weights':['uniform'],
'n_neighbors':[i for i in range(1,11)]
},
{
'weights':['distance'],
'n_neighbors':[i for i in range(1,11)],
'p':[i for i in range(1,6)]
}
]
knn_clf = KNeighborsClassifier()
grid_search = GridSearchCV(knn_clf,param_grid,cv=2,n_jobs=-1,verbose=2)
# n_jobs 分配几个核进行并行处理,默认为1,-1表应用所有核
# verbose 搜索过程中进行输出,便于及时了解搜索状态(值越大,越详细)
%%time grid_search.fit(X_train,y_train) # 耗时长
grid_search.best_estimator_ # = knn_clf
'''
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=3, p=2,
weights='uniform')
'''
grid_search.best_score_ # 0.9860821155184412
grid_search.best_params_ # {'n_neighbors': 3, 'weights': 'uniform'}
knn_clf.score(X_test,y_test) # 0.9861111111111112
线性回归法 Linear Regression
解决回归问题(连续空间,预测一个数值),思想简单,容易实现(是许多强大的非线性模型的基础), 结果具有很好的可解释性
寻找一条直线,最大程度的“拟合”样本特征和样本输出标记之间的关系
损失函数 loss function (or 效用函数 utility function) => 用于训练模型
- 衡量 预测值 $y_{predict}^{(i)}$ 与 真实值 $y_{true}^{(i)}$ 之间的差距:
- $\sum_{i=1}^m{|y_{predict}^{(i)} - y_{true}^{(i)}|}$ : 不可导
- $\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2}$ : 可导
- 目标:差距尽可能的小
- 方法:求导,导数为0处即为极值处
- 衡量 预测值 $y_{predict}^{(i)}$ 与 真实值 $y_{true}^{(i)}$ 之间的差距:
vs
kNN:LinearRegression kNN 典型的参数学习 非参数学习 只能解决回归问题 可用于解决回归和分类问题 对数据有假设:线性 对数据没有假设
线性回归算法的评测
- 平均绝对误差
MAE(Mean Absolute Error),与样本数m无关- $\frac{1}{m}\sum_{i=1}^m{|y_{predict}^{(i)} - y_{true}^{(i)}|}$
- 均方误差
MSE(Mean Squared Error),与样本数m无关- $\frac{1}{m}\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2}$
- 均方根误差
RMSE(Root Mean Squared Error), 量纲一致- $\sqrt{ \frac{1}{m}\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2} } = \sqrt{MSE}$
- 结果值要比
MAE大些,RMSE中的平方有放大误差的趋势,而MAE没有这样的趋势,从某种意义上,RMSE更小即让误差大的更小
注:
- 原本计算误差(损失函数) $\sum_{i=1}^m{|y_{predict}^{(i)} - y_{true}^{(i)}|}$ 或 $\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2}$
- 总值受m数影响,平方后量纲不对(例如原本是米,现在是平方米)
$R^2$:
R Squared(与准确度accurancy相比,存在小于0的情况)- $R^2 = 1 - \frac{SS_{residual}}{SS_{total}} = 1 - \frac{ \sum_i{(y^{(i)}-y_{true}^{(i)})^2} }{ \sum_i{(\overline{y_{true}}-y_{true}^{(i)})^2} } = 1 - \frac{ \frac{1}{m} \sum_i{(y^{(i)}-y_{true}^{(i)})^2} }{ \frac{1}{m} \sum_i{(\overline{y_{true}}-y_{true}^{(i)})^2} } = 1 - \frac{MSE(y,y_{true})}{Var(y_{true})}$
- $SS_{residual}$: Residual Sum of Squares, 使用
模型(充分考虑了x与y的关系)预测产生的误差 - $SS_{total}$: Total Sum of Squares, 使用
基准模型BaselineModel($y=\overline{y}$,与x无关)预测产生的误差
- $SS_{residual}$: Residual Sum of Squares, 使用
- $R^2<=1$,越大越好
=1: 无错误,最好=0: 等于BaselineModel<0: 说明学习到的模型还不如BaselineModel(此时,很可能数据不存在任何线性关系)
- $R^2 = 1 - \frac{SS_{residual}}{SS_{total}} = 1 - \frac{ \sum_i{(y^{(i)}-y_{true}^{(i)})^2} }{ \sum_i{(\overline{y_{true}}-y_{true}^{(i)})^2} } = 1 - \frac{ \frac{1}{m} \sum_i{(y^{(i)}-y_{true}^{(i)})^2} }{ \frac{1}{m} \sum_i{(\overline{y_{true}}-y_{true}^{(i)})^2} } = 1 - \frac{MSE(y,y_{true})}{Var(y_{true})}$
最小二乘法
$$
\begin{split}
y_{predict}^{(i)} & = ax^{(i)}+b \\
J(a,b) &= \sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2} \\
\end{split}
$$
$$ \Rightarrow J(a,b)= \sum_{i=1}^m{(ax^{(i)}+b) - y_{true}^{(i)})^2} \\ $$
$$ \begin{cases} \frac{\partial J(a,b)}{\partial a} = 0 & \Rightarrow a = \frac{\sum_{i=1}^m{(x^{(i)}y^{(i)}-x^{(i)}\overline{y_{true}})}}{\sum_{i=1}^m{(({x^{(i)}})^2-\overline{x}x^{(i)})}} = \frac{\sum_{i=1}^m{(x^{(i)}-\overline{x})(y^{(i)}-\overline{y_{true}})}}{\sum_{i=1}^m{(x^{(i)}-\overline{x})^2}} \\ \frac{\partial J(a,b)}{\partial b} = 0 & \Rightarrow b = \frac{ \sum_{i=1}^m{y_{true}^{(i)} - a\sum_{i=1}^n{x^{(i)}}} }{n} = \overline{y_{true}}-a\overline{x} \\ \end{cases} \\ (m个样本) $$
向量化运算 ($\overrightarrow{w} \cdot \overrightarrow{v}$)
$$ \begin{split} a & =\frac{\sum_{i=1}^m{(x^{(i)}-\overline{x})(y^{(i)}-\overline{y_{true}})}}{\sum_{i=1}^m{(x^{(i)}-\overline{x})^2}} \\ & =\frac{ \sum_{i=1}^m{w^{(i)} v^{(i)}} }{ \sum_{i=1}^m{w^{(i)} w^{(i)}} } & \begin{cases} w^{(i)} = (x^{(i)}-\overline{x}) \\ v^{(i)} = (y^{(i)}-\overline{y_{true}}) \end{cases} \\ & =\frac{\overrightarrow{w} \cdot \overrightarrow{v}}{\overrightarrow{w} \cdot \overrightarrow{w}} & \begin{cases} \overrightarrow{w} = (w^{(1)},w^{(2)},...,w^{(m)}) \\ \overrightarrow{v} = (v^{(1)},v^{(2)},...,v^{(m)}) \\ \end{cases} \end{split} $$
Sample: 自实现的简单线性回归(样本特征只有一个)预测
import numpy as np
class SimpleLinearRegression:
def __init__(self):
self.a_ = None
self.b_ = None
def fit(self,x_train,y_train):
assert x_train.ndim == 1, "Simple Linear Regressor can only solve single feature training data."
assert len(x_train) == len(y_train), "the size of x_train must be equal to the size of y_train."
x_mean = np.mean(x_train)
y_mean = np.mean(y_train)
# method1:
# num = 0.0 # 计算a的分母
# d = 0.0 # 计算a的分子
# for x_i,y_i in zip(x_train,y_train):
# num += (x_i - x_mean) * (y_i - y_mean)
# d += (x_i-x_mean) ** 2
# method2: 向量化运算(性能更优)
num = (x_train - x_mean).dot(y_train - y_mean)
d = (x_train - x_mean).dot(x_train - x_mean)
self.a_ = num / d
self.b_ = y_mean - self.a_ * x_mean
return self
def predict(self,x_predict):
assert x_predict.ndim == 1, "Simple Linear Regressor can only solve single feature training data."
assert self.a_ is not None and self.b_ is not None, "must fit before predict!"
return self.a_ * x_predict + self.b_
def test_randomData():
# 1. data
# x_train = np.linspace(1,5,5)
# y_train = np.array([1,3,2,3,5],dtype=float)
m=10
x_train=np.random.random(size=m)
y_train=x_train*2.0+3.0+np.random.normal(size=m)
# 2. LinearRegression
reg = SimpleLinearRegression()
reg.fit(x_train,y_train)
print("a=%f,b=%f" % (reg.a_,reg.b_))
x_predict = np.array([0.6])
y_predict = reg.predict(x_predict)
print(y_predict)
# 3. visualization
import matplotlib.pyplot as plt
# y_hat = reg.a_ * x_train + reg.b_
y_hat = reg.predict(x_train)
plt.scatter(x_train,y_train)
plt.plot(x_train,y_hat,color='r')
plt.scatter(x_predict,y_predict,color='g')
plt.show()
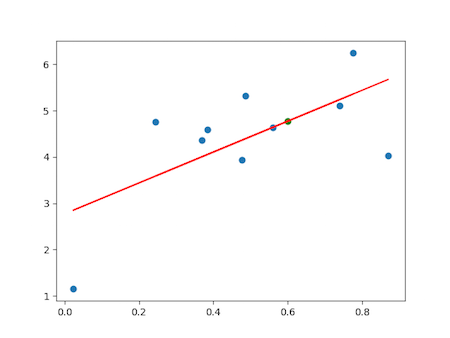
评测算法
均方误差
MSE(Mean Squared Error): $\frac{1}{m}\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2}$mse = np.sum((y_predict-y_test)**2)/len(y_test)均方根误差
RMSE(Root Mean Squared Error): $\sqrt{ \frac{1}{m}\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2} } = \sqrt{MSE}$rmse = np.sqrt(mse)平均绝对误差
MAE(Mean Absolute Error): $\frac{1}{m}\sum_{i=1}^m{|y_{predict}^{(i)} - y_{true}^{(i)}|}$mae = np.sum(np.abs(y_predict-y_test))/len(y_test)R Squared: $1 - \frac{ \sum_i{(y^{(i)}-y_{true}^{(i)})^2} }{ \sum_i{(\overline{y_{true}}-y_{true}^{(i)})^2} } = 1 - \frac{ \frac{1}{m} \sum_i{(y^{(i)}-y_{true}^{(i)})^2} }{ \frac{1}{m} \sum_i{(\overline{y_{true}}-y_{true}^{(i)})^2} } = 1 - \frac{MSE(y,y_{true})}{Var(y_{true})}$r2 = 1 - mean_squared_error(y_test,y_predict)/np.var(y_test)sklearn中的
MSE,MAE(无RMSE),R Squaredfrom sklearn.metrics import mean_squared_error from sklearn.metrics import mean_absolute_error from sklearn.metrics import r2_score mse = mean_squared_error(y_test,y_predict) rmse = np.sqrt(mean_squared_error(y_test,y_predict)) mae = mean_absolute_error(y_test,y_predict) r2_score = r2_score(y_test,y_predict)
Sample:
def test_bostonData():
# 1. data
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston() # 波士顿房产数据
x = boston.data[:,5] # 只使用‘RM’房间数量这个特征
y = boston.target
# 数据集清洗:去除最大值的点(采集样本的上限点,可能不是真实的点)
y_max=np.max(y)
x = x[y<y_max]
y = y[y<y_max]
print("x.shape=%s,y.shape=%s" % (x.shape,y.shape))
# train test split
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=66)
print("x_train.shape=%s,x_test.shape=%s" % (x_train.shape,x_test.shape))
# 2. LinearRegression
reg = SimpleLinearRegression()
reg.fit(x_train,y_train)
print("a=%f,b=%f" % (reg.a_,reg.b_))
y_predict = reg.predict(x_test)
# 3. score
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
mse = mean_squared_error(y_test,y_predict)
rmse = root_mean_squared_error(y_test,y_predict)
mae = mean_absolute_error(y_test,y_predict)
r2 = r2_score(y_test,y_predict)
print("mse=%f,rmse=%f,mae=%f,r2=%f" % (mse,rmse,mae,r2))
# 4. visualization
import matplotlib.pyplot as plt
y_hat = reg.predict(x_train)
plt.scatter(x_train,y_train)
plt.scatter(x_test,y_test,color='g')
plt.plot(x_train,y_hat,color='r')
plt.show()
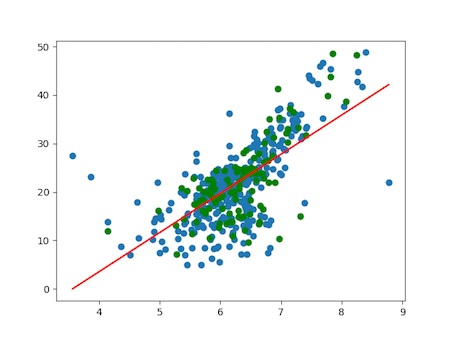
多元线性回归
$$
\begin{align}
& & y_{predict}^{(i)} & = θ_0 + θ_1x_1^{(i)} + θ_2x_2^{(i)} + ... + θ_nx_n^{(i)} \\
& & & = θ_0x_0^{(i)} + θ_1x_1^{(i)} + θ_2x_2^{(i)} + ... + θ_nx_n^{(i)} \\
& & & = \overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} &
\begin{cases}
\overrightarrow{x}^{(i)} = (x_0^{(i)},x_1^{(i)}, x_2^{(i)}, ..., x_n^{(i)}) &, x_0^{(i)} \equiv 1 \\
\overrightarrow{θ} = (θ_0,θ_1,θ_2,...,θ_n)
\end{cases} \\
\\
\Longrightarrow & & y_{predict} & = X \cdot \Theta \\
\\
& & \begin{pmatrix}
y_{predict}^{(1)} \\
y_{predict}^{(2)} \\
... \\
y_{predict}^{(m)} \\
\end{pmatrix}
& = \begin{pmatrix}
1 & x_1^{(1)} & x_2^{(1)} & ... & x_n^{(1)} \\
1 & x_1^{(2)} & x_2^{(2)} & ... & x_n^{(2)} \\
... \\
1 & x_1^{(m)} & x_2^{(m)} & ... & x_n^{(m)} \\
\end{pmatrix}
\cdot
\begin{pmatrix}
θ_0 \\
θ_1 \\
θ_2 \\
... \\
θ_n \\
\end{pmatrix} \\
\\
\Longrightarrow & & 目标: & 找到θ_0,θ_1,θ_2,...,θ_n, 使得\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2} 尽可能的小
\end{align}
$$
目标: 找到$θ_0,θ_1,θ_2,...,θ_n$,使得$\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2}$ 尽可能的小 ( 即$(y_{predict} - y_{true})^T \cdot (y_{predict} - y_{true})$ 尽可能的小 )
$(θ_0,θ_1,θ_2,...,θ_n)$:
- $θ_0$ : 截距 intercept
- $θ_1,θ_2,...,θ_n$ : 系数 coefficients
Sample:自定义实现(使用正规方程解 Normal Equation)
- $\Theta = (X^TX)^{-1}X^Ty_{true}$
- 问题:时间复杂度高,O(n^3),优化后可达到O(n^2.4)
- 优点:不需要对数据做归一化处理
import numpy as np
from metrics import r2_score
class LinearRegression:
def __init__(self):
self.__theta = None
self.intercept_ = None # 截距 intercept
self.coef_ = None # 系数 coefficients
# 正规方程解(Normal Equation)
def fit_normal(self,X_train,y_train):
assert X_train.shape[0] == y_train.shape[0],"the size of X_train must be equal to the size of y_train"
X_b = np.hstack([np.ones(shape=(X_train.shape[0],1)),X_train])
self.__theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.intercept_ = self.__theta[0]
self.coef_ = self.__theta[1:]
return self
def predict(self,X_predict):
assert self.intercept_ is not None and self.coef_ is not None,"must fit before predict!"
assert X_predict.shape[1] == len(self.coef_),"the feature number of X_predict must be equal to X_train"
X_b = np.hstack([np.ones(shape=(X_predict.shape[0],1)),X_predict])
return X_b.dot(self.__theta)
def score(self,X_test,y_test):
y_predict = self.predict(X_test)
return r2_score(y_test,y_predict)
def __repr__(self):
return "LinearRegression()"
if __name__ == '__main__':
# 1. data
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston()
X = boston.data
y = boston.target
y_max = np.max(y)
X = X[y<y_max]
y = y[y<y_max]
print("X.shape:",X.shape)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=66)
print("X_train.shape:",X_train.shape)
# 2. LinearRegression
reg = LinearRegression()
reg.fit_normal(X_train,y_train)
print("coef_:",reg.coef_)
print("intercept_:",reg.intercept_)
# y_predict = reg.predict(X_test)
r2 = reg.score(X_test,y_test)
print("r2:",r2)
# 3. coefficents meaning
print("features:\n",boston.feature_names)
coefInds = np.argsort(reg.coef_)
print("(important)sorted features:\n",boston.feature_names[coefInds])
scikit-learn中的LinearRegression
内部使用梯度下降法训练模型
# 1. data
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston()
X = boston.data
y = boston.target
y_max = np.max(y)
X = X[y<y_max]
y = y[y<y_max]
print("X.shape:",X.shape)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=66)
print("X_train.shape:",X_train.shape)
# 2. LinearRegression
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
reg.fit(X_train,y_train)
print("coef_:%s,intercept_:%s" % (reg.coef_,reg.intercept_))
r2 = reg.score(X_test,y_test)
print("r2:",r2)
scikit-learn中的SGDRegressor
内部使用随机梯度下降法训练模型
# 1. data
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston()
X = boston.data
y = boston.target
y_max = np.max(y)
X = X[y<y_max]
y = y[y<y_max]
print("X.shape:",X.shape)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=66)
print("X_train.shape:",X_train.shape)
#进行数据归一化
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(n_iter=10)
sgd_reg.fit(X_train_standard,y_train)
print("coef_:%s,intercept_:%s" % (sgd_reg.coef_,sgd_reg.intercept_))
r2 = sgd_reg.score(X_test_standard,y_test)
print("r2:",r2)
梯度下降法(Gradient Descent)
梯度下降/上升法:
是一种基于搜索的最优化方法 => 最优化一个目标函数使用的方法(本身不是一个机器学习算法)
梯度
∇J(θ):- 目标函数
J(θ),θ为模型参数 - 导数:
- 代表斜率(曲线方程中,代表切线斜率)
- 代表方向,对应目标函数增大的方向(负: 在减少,正: 在增大)
- 梯度(对每个维度的θ求导): $∇J(θ) = (\frac{\partial J}{\partial θ_0},\frac{\partial J}{\partial θ_1},...,\frac{\partial J}{\partial θ_n})$
- 目标函数
η∇J(θ)- 梯度下降法: 最小化一个损失函数 (loss function) $θ^{i+1} = θ^i + (- η∇J(θ^i))$
- 梯度上升法:最大化一个效用函数 (utility function) $θ^{i+1} = θ^i + (η∇J(θ^i))$
- 超参数:
- 学习率(learning reate)
η- 梯度移动步长
- 取值影响获得最优解的速度(取值不合适,甚至得不到最优解)
- 太小:减慢收敛学习速度
- 太大:可能导致不收敛
- 初始$θ^1$:
- 不是所有函数都有唯一的极值点(局部最优解,全局最优解)
- 解决方案:多次运行,随机化初始点
- 学习率(learning reate)
计算梯度时使用样本的策略:
批量(Batch) 随机(Stochastic) 小批量(Mini-Batch) 每次对所有样本求梯度 每次对一个样本求梯度 每次对 k个样本求梯度慢,方向确定(稳定) 快,方向不确定(不稳定) 中和前两个方法的优缺点 eg: 批量梯度下降法 (Batch Gradient Descent) eg: 随机梯度下降法 (Stochastic Gradient Descent) eg: 小批量梯度下降法 (Mini-Batch Gradient Descent) - 随机的意义:
- 跳出局部最优解
- 更快的运行速度
- 机器学习领域很多算法都使用了随机的特点,如:随机搜索,随机森林
- 随机的意义:
批量梯度下降法(Batch Gradient Descent)
批量梯度下降法θ = θ - η∇J(θ):
- 使用所有样本,训练模型
- 结果是一个向量,可以表达搜索方向
Sample: 线性回归中使用的梯度下降法
- 线性回归函数(模型):
y = X·θ - 损失函数:
J(θ)- $J(θ) = \sum_{i=1}^m{(y_{predict}^{(i)}-y_{true}^{(i)})^2}$ 与样本数量有关
- $J(θ) = \frac{1}{m}\sum_{i=1}^m{(y_{predict}^{(i)}-y_{true}^{(i)})^2} = MSE(y_{predict},y_{true})$ 使用这种,与样本数量无关
- 梯度:
∇J(θ)
$$
\begin{align}
& & J(θ) & = \frac{1}{m}\sum_{i=1}^m{(y_{predict}^{(i)} - y_{true}^{(i)})^2}
\qquad \qquad
y_{predict} = X·θ \\
& & & = \frac{1}{m}\sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})^2}
\qquad
\begin{cases}
\overrightarrow{x}^{(i)} = (x_0^{(i)},x_1^{(i)}, x_2^{(i)}, ..., x_n^{(i)}) \, x_0^{(i)} \equiv 1 \\
\overrightarrow{θ} = (θ_0,θ_1,θ_2,...,θ_n) \\
\end{cases} \\
\\ \Longrightarrow
& & ∇J(θ)& = \begin{pmatrix}
\frac{\partial J}{\partial θ_0} \\
\frac{\partial J}{\partial θ_1} \\
\frac{\partial J}{\partial θ_2} \\
... \\
\frac{\partial J}{\partial θ_n} \\
\end{pmatrix}
= \frac{1}{m}
\begin{pmatrix}
\sum_{i=1}^m{2(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_0^{(i)}} \\
\sum_{i=1}^m{2(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_1^{(i)}} \\
\sum_{i=1}^m{2(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_2^{(i)}} \\
... \\
\sum_{i=1}^m{2(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_n^{(i)}} \\
\end{pmatrix}
= \frac{2}{m}
\begin{pmatrix}
\sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_0^{(i)}} \\
\sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_1^{(i)}} \\
\sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_2^{(i)}} \\
... \\
\sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_n^{(i)}} \\
\end{pmatrix} \\
& & & = \frac{2}{m}
\begin{pmatrix}
\overrightarrow{w} \cdot \overrightarrow{x_0} \\
\overrightarrow{w} \cdot \overrightarrow{x_1} \\
... \\
\overrightarrow{w} \cdot \overrightarrow{x_n} \\
\end{pmatrix}
\qquad
\begin{cases}
\overrightarrow{w} = (
\overrightarrow{x}^{(1)} \cdot \overrightarrow{θ} - y_{true}^{(1)},
\overrightarrow{x}^{(2)} \cdot \overrightarrow{θ} - y_{true}^{(2)},
...,
\overrightarrow{x}^{(m)} \cdot \overrightarrow{θ} - y_{true}^{(m)}
) \\
\overrightarrow{x_j} = (x_j^1,x_j^2,...,x_j^m) \qquad, j \in [0,n] \\
\end{cases}
\\
& & & = \frac{2}{m}(X \cdot \Theta - y_{true})^T \cdot X
\qquad : matrix[1_m] \cdot matrix[m_(n+1)] \rightarrow matrix[1_(n+1)] \\
& & & = \frac{2}{m} X^T \cdot (X \cdot \Theta - y_{true})
\qquad : matrix[(n+1)_m] \cdot matrix[m_1] \rightarrow matrix[(n+1)_1] \\
\end{align}
$$
- 线性回归中的损失函数具有唯一最优解
- 注意:使用梯度下降法前,最好进行数据归一化
自定义实现LinearRegression:
(sklearn中的LinerRegression也是使用Gradient Descent训练模型)
class LinearRegression:
def __init__(self):
self.__theta = None
self.intercept_ = None # 截距 intercept
self.coef_ = None # 系数 coefficients
# 使用正规方程解(Normal Equation)训练模型
def fit_normal(self,X_train,y_train):
assert X_train.shape[0] == y_train.shape[0],"the size of X_train must be equal to the size of y_train"
X_b = np.hstack([np.ones(shape=(X_train.shape[0],1)),X_train])
self.__theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
self.intercept_ = self.__theta[0]
self.coef_ = self.__theta[1:]
return self
# 使用梯度下降法(Gradient Descent)训练模型
def fit_gd(self,X_train,y_train,eta=0.01,n_iters=1e4):
assert X_train.shape[0]==y_train.shape[0],"the size of X_train must be equal to the size of y_train"
# loss function: J(θ)
def J(theta,X_b,y_true):
try:
return np.sum((X_b.dot(theta)-y_true)**2)/len(y_true)
except:
return float("inf")
# derivative: ∇J(θ) = J(θ)' = dJ/dθ = (2/m)·X^T·(X·θ - y_true)
def dJ(theta,X_b,y_true):
# res = np.empty(len(theta))
# res[0] = np.sum(X_b.dot(theta)-y_true)
# for i in range(1,len(theta)):
# res[i] = (X_b.dot(theta)-y_true).dot(X_b[:,i])
# return (res * 2)/len(X_b)
return X_b.T.dot(X_b.dot(theta)-y_true)*2/len(y_true)
# gradient_descent: -η∇J(θ) ≅ 0
def gradient_descent(X_b,y_true,initial_theta,eta,epsilon=1e-8,n_iters=1e4):
theta = initial_theta
i_iter = 0
while i_iter<n_iters:
gradient = dJ(theta,X_b,y_true)
last_theta = theta
theta = theta - eta * gradient
if abs(J(theta,X_b,y_true)-J(last_theta,X_b,y_true)) < epsilon:
break;
i_iter+=1
return theta
X_b = np.hstack([np.ones(shape=(len(X_train),1)),X_train]) # m*n matrix => m*(1+n) matrix
initial_theta = np.zeros(shape=(X_b.shape[1])) # n features = X_b col numbers
self.__theta = gradient_descent(X_b,y_train,initial_theta,eta)
self.intercept_ = self.__theta[0]
self.coef_ = self.__theta[1:]
return self
def predict(self,X_predict):
assert self.intercept_ is not None and self.coef_ is not None,"must fit before predict!"
assert X_predict.shape[1] == len(self.coef_),"the feature number of X_predict must be equal to X_train"
X_b = np.hstack([np.ones(shape=(X_predict.shape[0],1)),X_predict])
return X_b.dot(self.__theta)
def score(self,X_test,y_test):
y_predict = self.predict(X_test)
return r2_score(y_test,y_predict)
def __repr__(self):
return "LinearRegression()"
def test_gradient_descent_fit():
# 1. data
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston()
X = boston.data
y = boston.target
y_max = np.max(y)
X = X[y<y_max]
y = y[y<y_max]
print("X.shape:",X.shape)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=66)
print("X_train.shape:",X_train.shape)
# 注意:使用梯度下降法前,最好进行数据归一化,防止overflow !
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
# 2. LinearRegression
reg = LinearRegression()
reg.fit_gd(X_train_standard,y_train)
print("coef_:",reg.coef_)
print("intercept_:",reg.intercept_)
# 3. predict/score
# y_predict = reg.predict(X_test_standard)
r2 = reg.score(X_test_standard,y_test)
print("r2:",r2)
# 4. coefficents meaning
print("features:\n",boston.feature_names)
coefInds = np.argsort(reg.coef_)
print(reg.coef_[coefInds])
print("(important)sorted features:\n",boston.feature_names[coefInds])
随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法θ = θ - η∇J(θ):
- 每次随机取一个样本,计算梯度(搜索的方向),训练模型
- 学习率
η- 固定值 => 模拟退火的思想: 随着循环次数的增加逐渐递减 $η = \frac{1}{\text{i_iters}} \rightarrow η = \frac{a}{\text{i_iters+b}}$
- 一般取
a = 5,b = 50
- 注:不能保证每次每次梯度都是减小的
Sample: 线性回归中使用随机梯度下降法
$$ \begin{align} & & ∇J(θ)& = \begin{pmatrix} \frac{\partial J}{\partial θ_0} \\ \frac{\partial J}{\partial θ_1} \\ \frac{\partial J}{\partial θ_2} \\ ... \\ \frac{\partial J}{\partial θ_n} \\ \end{pmatrix} = \frac{2}{m} \begin{pmatrix} \sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_0^{(i)}} \\ \sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_1^{(i)}} \\ \sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_2^{(i)}} \\ ... \\ \sum_{i=1}^m{(\overrightarrow{x}^{(i)} \cdot \overrightarrow{θ} - y_{true}^{(i)})x_n^{(i)}} \\ \end{pmatrix} \\ \\ \Longrightarrow & & & 2 \begin{pmatrix} (\overrightarrow{x}^{(k)} \cdot \overrightarrow{θ} - y_{true}^{(k)}) \cdot x_0^{(k)} \\ (\overrightarrow{x}^{(k)} \cdot \overrightarrow{θ} - y_{true}^{(k)}) \cdot x_1^{(k)} \\ ... \\ (\overrightarrow{x}^{(k)} \cdot \overrightarrow{θ} - y_{true}^{(k)}) \cdot x_n^{(k)} \\ \end{pmatrix} \\ & & & = 2 (\overrightarrow{x}^{(k)} \cdot \overrightarrow{θ} - y_{true}^{(k)}) \cdot \overrightarrow{x}^{(k)} & \begin{cases} \overrightarrow{x}^{(k)} : (n+1)维行向量 \\ (\overrightarrow{x}^{(k)} \cdot \overrightarrow{θ} - y_{true}^{(k)}) : 一个标量 \\ k = random(1,m) \in [1,m] \end{cases} \\ & & & = 2 (x^{(k)})^T \cdot (\overrightarrow{x}^{(k)} \cdot \overrightarrow{θ} - y_{true}^{(k)}) & \rightarrow matrix[(n+1)*1] : n+1维列向量 \\ \end{align} $$
自定义实现LinearRegression:
(sklearn中的SGDRegressor使用Stochastic Gradient Descent训练模型)
# 使用随机梯度下降法(Stochastic Gradient Descent)训练模型
# n_iters 整体样本处理几轮
def fit_sgd(self,X_train,y_train,n_iters=5,t0=5,t1=50):
assert X_train.shape[0]==y_train.shape[0],"the size of X_train must be equal to the size of y_train"
assert n_iters >0,"n_iters should be greater 0"
def dJ_sgd(theta,X_b_i,y_i):
return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2
def sdg(X_b,y,initial_theta,n_iters,t0=t0,t1=t1):
def learning_rate(t):
return t0/(t+t1)
theta = initial_theta
m = len(X_b)
for cur_iter in range(n_iters):
indexes = np.random.permutation(m)
X_b_new = X_b[indexes]
y_new = y[indexes]
for i in range(m):
gradient = dJ_sgd(theta,X_b_new[i],y_new[i])
theta = theta - learning_rate(cur_iter*m+i)*gradient
return theta
X_b = np.hstack([np.ones(shape=(len(X_train),1)),X_train]) # m*n matrix => m*(1+n) matrix
initial_theta = np.random.randn(X_b.shape[1]) # n features = X_b col numbers
self.__theta = sdg(X_b,y_train,initial_theta,n_iters,t0,t1)
self.intercept_ = self.__theta[0]
self.coef_ = self.__theta[1:]
return self
def test_sdg_fit():
# # 1. data
# m = 10000
# x = np.random.normal(size=m)
# X = x.reshape(-1,1)
# y = 4.*x + 3. + np.random.normal(0,3,size=m)
# # 2. fit_sdg
# reg = LinearRegression()
# reg.fit_sgd(X,y,n_iters=2)
# print("coef_:",reg.coef_)
# print("intercept_:",reg.intercept_)
# 1. data
from sklearn import datasets
from sklearn.model_selection import train_test_split
boston = datasets.load_boston()
X = boston.data
y = boston.target
y_max = np.max(y)
X = X[y<y_max]
y = y[y<y_max]
print("X.shape:",X.shape)
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=66)
print("X_train.shape:",X_train.shape)
# 注意:使用梯度下降法前,最好进行数据归一化,防止overflow
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
# 2. LinearRegression
reg = LinearRegression()
reg.fit_sgd(X_train_standard,y_train,n_iters=10)
print("coef_:",reg.coef_)
print("intercept_:",reg.intercept_)
# 3. predict/score
# y_predict = reg.predict(X_test_standard)
r2 = reg.score(X_test_standard,y_test)
print("r2:",r2)
# 4. coefficents meaning
print("features:\n",boston.feature_names)
coefInds = np.argsort(reg.coef_)
print(reg.coef_[coefInds])
print("(important)sorted features:\n",boston.feature_names[coefInds])
梯度调试
模拟导数:验证求导是否正确,比直接求导慢的多,只是用于检查验证
$$ \begin{align} \frac{dJ}{dθ} & = \frac{J(θ+ε)-J(θ-ε)}{2ε} & θ = (θ_0,θ_1,θ_2,...,θ_n) \\ \\ ∇J(θ) & = \frac{\partial J}{\partial θ} = \begin{pmatrix} \frac{\partial J}{\partial θ_0} \\ \frac{\partial J}{\partial θ_1} \\ \frac{\partial J}{\partial θ_2} \\ ... \\ \frac{\partial J}{\partial θ_n} \\ \end{pmatrix} = \begin{pmatrix} \frac{J(θ_0^+)-J(θ_0^-)}{2ε} \\ \frac{J(θ_1^+)-J(θ_1^-)}{2ε} \\ \frac{J(θ_2^+)-J(θ_2^-)}{2ε} \\ ... \\ \frac{J(θ_n^+)-J(θ_n^-)}{2ε} \\ \end{pmatrix} & \begin{cases} θ_0^+ = (θ_0+ε,θ_1,θ_2,...,θ_n) & , θ_0^- = (θ_0-ε,θ_1,θ_2,...,θ_n) \\ θ_1^+ = (θ_0,θ_1+ε,θ_2,...,θ_n) & , θ_1^- = (θ_0,θ_1-ε,θ_2,...,θ_n) \\ ... \\ θ_n^+ = (θ_0,θ_1,θ_2,...,θ_n+ε) & , θ_j^- = (θ_0,θ_1,θ_2,...,θ_n-ε) \\ \end{cases} \end{align} $$
# loss function: J(θ)
def J(theta,X_b,y_true):
try:
return np.sum((X_b.dot(theta)-y_true)**2)/len(y_true)
except:
return float("inf")
# derivative: ∇J(θ) = dJ/dθ = (2/m)·X^T·(X·θ - y_true)
def dJ_math(theta,X_b,y_true):
return X_b.T.dot(X_b.dot(theta)-y_true)*2/len(y_true)
# derivative: ∇J(θ) = dJ/dθ : (J(θ+ε)-J(θ-ε))/2ε
def dJ_debug(theta,X_b,y_true,epsilon=0.01):
res = np.empty(len(theta))
for i in range(len(theta)):
theta_1 = theta.copy()
theta_2 = theta.copy()
theta_1[i] += epsilon
theta_2[i] -= epsilon
res[i] = (J(theta_1,X_b,y)-J(theta_2,X_b,y))/(2*epsilon)
return res
# 1. data
np.random.seed(666)
X = np.random.random(size=(1000,10))
true_theta = np.arange(1,12,dtype=float)
# array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11.])
X_b = np.hstack([np.ones((len(X),1)),X])
y = X_b.dot(true_theta) + np.random.normal(size=(1000))
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01
# 2. use dJ_debug
theta_debug = gradient_descent(dJ_debug,X_b,y,initial_theta,eta)
print(theta_debug)
'''
CPU times: user 8.66 s, sys: 137 ms, total: 8.8 s
Wall time: 4.65 s
array([ 1.1251597 , 2.05312521, 2.91522497, 4.11895968, 5.05002117,
5.90494046, 6.97383745, 8.00088367, 8.86213468, 9.98608331,
10.90529198])
'''
# 3. use dJ_match
theta_math = gradient_descent(dJ_math,X_b,y,initial_theta,eta)
print(theta_math)
'''
CPU times: user 1.2 s, sys: 18.5 ms, total: 1.22 s
Wall time: 645 ms
array([ 1.1251597 , 2.05312521, 2.91522497, 4.11895968, 5.05002117,
5.90494046, 6.97383745, 8.00088367, 8.86213468, 9.98608331,
10.90529198])
'''
# => then check and compare the result : theta_debug & theta_math
PCA
主成分分析法
对数据进行降维 内部可使用梯度上升法(搜索策略)实现